Understanding the intriguing concept of a reciprocal of negative number is easier than you might think. In mathematics, fractions often play a crucial role, and a negative number’s reciprocal is simply another facet of fraction-based operations. Many students learning through tools like Khan Academy, often find these concepts tricky, but with our simple guide, you’ll have a grasp on the fundamentals in no time. Reciprocal of negative number is an important building block, applicable when one is working with concepts in algebra.
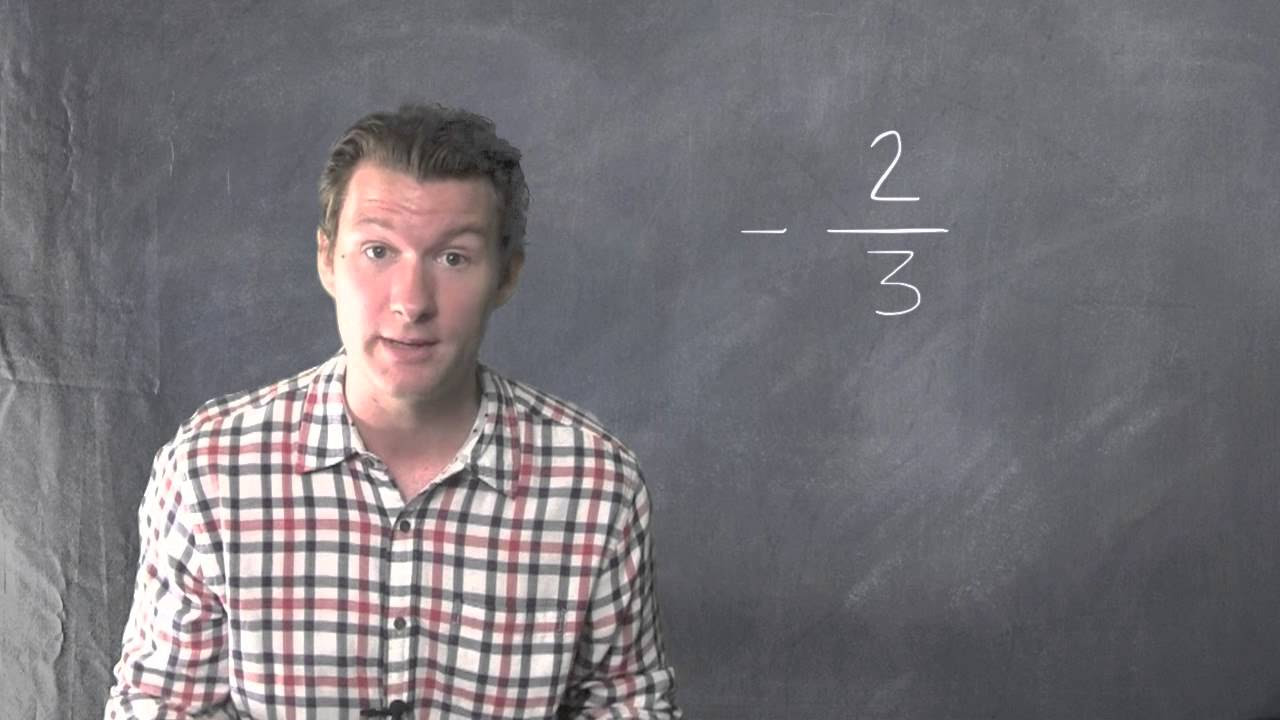
Image taken from the YouTube channel David May , from the video titled What is a Negative Reciprocal? | Dave May Teaches .
Reciprocals are a fundamental concept in mathematics, playing a vital role in simplifying equations and solving problems across various mathematical disciplines. At its core, a reciprocal is simply the inverse of a number.
While the idea of reciprocals is straightforward for positive numbers, a cloud of confusion often forms when negative numbers enter the equation. Many students and even seasoned mathematicians sometimes stumble when asked to find the reciprocal of a negative number. Is it positive? Is it negative? Does the negative sign even matter?
What is a Reciprocal? A Matter of Inversion
In the simplest terms, the reciprocal of a number is what you multiply that number by to get 1. It’s an inversion – flipping the number over.
For example, the reciprocal of 2 is 1/2, because 2 * (1/2) = 1. Similarly, the reciprocal of 3/4 is 4/3.
The Importance of Reciprocals in Mathematics
Reciprocals aren’t just abstract concepts; they’re essential tools in mathematics. They are used extensively in:
- Division: Dividing by a number is the same as multiplying by its reciprocal. This is particularly useful when dealing with fractions.
- Solving Equations: Reciprocals help isolate variables and simplify complex equations.
- Trigonometry: Reciprocal trigonometric functions (cosecant, secant, cotangent) are defined using reciprocals.
- Calculus: Reciprocals appear in derivatives and integrals.
Addressing the Negative Reciprocal Misconception
The most common mistake when dealing with negative reciprocals is confusion about the sign. Many people mistakenly believe that the reciprocal of a negative number should be positive.
However, the reciprocal of a negative number is always negative. This stems from the rule that a negative times a negative is a positive. To get a positive result (1), you need to multiply a negative number by another negative number.
Your Guide to Negative Reciprocals
This guide aims to provide a clear, concise, and easy-to-understand explanation of how to find the reciprocal of negative numbers. We’ll break down the concept, step by step, with plenty of examples to solidify your understanding.
By the end of this guide, you’ll be able to confidently tackle any negative reciprocal problem that comes your way. Prepare to demystify the negative reciprocal!
Reciprocals aren’t just abstract concepts; they’re essential tools in mathematics. They are used extensively in:
Division: Dividing by a number is the same as multiplying by its reciprocal. This is particularly useful when dealing with fractions.
Solving Equations: Reciprocals help isolate variables and simplify complex equations.
Trigonometry: Reciprocal trigonometric functions (cosecant, secant, cotangent) are defined using reciprocals.
Calculus: Reciprocals appear in derivatives and integrals.
To properly grasp the intricacies of negative reciprocals, it’s essential to first solidify our understanding of reciprocals in their basic form, particularly concerning positive numbers. Let’s revisit the fundamental definition and explore examples with positive numbers before venturing into the negative realm.
Reciprocal Fundamentals: A Quick Review
Before tackling the quirks of negative reciprocals, let’s ensure a firm grasp of the basics. We’ll begin by clearly defining what a reciprocal is, then explore practical examples using positive numbers. This foundational understanding is crucial before introducing the added complexity of negative signs.
Defining Reciprocals: The Inversion Principle
At its core, a reciprocal represents the inverse of a number. More precisely:
The reciprocal of a number, x, is the value that, when multiplied by x, results in 1. This crucial value is often denoted as 1/x.
Think of it as "flipping" the number. If you have a whole number, its reciprocal is one over that number. If you have a fraction, you simply swap the numerator and denominator.
This "flipping" or inverting is the essence of finding a reciprocal. Let’s look at how to practically apply this principle.
How to Find a Reciprocal
The process is quite straightforward:
- Express the number as a fraction: If it’s a whole number, put it over 1 (e.g., 5 becomes 5/1).
- Invert the fraction: Swap the numerator and denominator.
- Simplify (if possible): Reduce the fraction to its simplest form.
This method works for both whole numbers and fractions, laying the groundwork for understanding reciprocals of negative numbers later on.
Reciprocals of Positive Numbers: Simple Examples
Let’s solidify your understanding with clear-cut examples using positive numbers. These examples show the simplicity of reciprocal calculation when dealing with positive values.
-
Example 1: The reciprocal of 2
2 can be written as 2/1.
Inverting this gives us 1/2.
Therefore, the reciprocal of 2 is 1/2. -
Example 2: The reciprocal of 1/2
This is already a fraction.
Inverting it gives us 2/1, which simplifies to 2.
Thus, the reciprocal of 1/2 is 2. -
Example 3: The reciprocal of 3/4
This is also already a fraction.
Inverting it gives us 4/3.
So, the reciprocal of 3/4 is 4/3.
A crucial point to remember: when you multiply any number by its reciprocal, the result is always 1. For instance:
- 2
**(1/2) = 1
- (1/2)** 2 = 1
- (3/4) * (4/3) = 1
This property of resulting in ‘1’ is a defining characteristic of reciprocals, regardless of whether they are positive or negative. Always remember to check your work.
Even with a strong grasp of basic reciprocals, understanding the nuances of negative reciprocals requires a solid foundation in negative numbers themselves. This understanding helps us visualize how these numbers behave and how they interact with the concept of inversion.
Negative Numbers Demystified: Building Context
Before diving into the reciprocals of negative numbers, it’s crucial to understand what negative numbers are and how they operate within the broader mathematical landscape.
What are Negative Numbers?
Negative numbers represent values less than zero.
They are located to the left of zero on the number line, mirroring positive numbers located on the right.
Think of a thermometer: temperatures below zero are represented by negative numbers.
This concept of "less than zero" might seem abstract.
Consider it as representing debt, a deficit, or a position below a certain reference point.
The further a negative number is from zero, the smaller its value. For example, -5 is smaller than -2.
Negative numbers are essentially the opposite of positive numbers.
Negative Numbers Within Number Systems
Negative numbers are integral parts of various number systems:
-
Integers: These include all whole numbers, both positive and negative, and zero (e.g., …, -3, -2, -1, 0, 1, 2, 3, …).
-
Rational Numbers: These are numbers that can be expressed as a fraction p/q, where p and q are integers and q is not zero. Rational numbers can be positive, negative, or zero (e.g., -1/2, -3/4, 5/2).
-
Negative rational numbers are simply fractions where the numerator or denominator (but not both) is negative.
-
For instance, -1/2 or 1/-2 are both valid representations of the same negative rational number.
-
Understanding these classifications helps contextualize negative numbers and their relationships with other types of numbers.
Basic Operations with Negative Numbers
The rules for basic arithmetic operations change slightly when dealing with negative numbers. Understanding these rules is vital for finding negative reciprocals:
-
Multiplication:
-
A negative number multiplied by a positive number results in a negative number (e.g., -2
**3 = -6).
-
A negative number multiplied by a negative number results in a positive number (e.g., -2** -3 = 6). This is a crucial rule to remember.
-
-
Division:
-
A negative number divided by a positive number results in a negative number (e.g., -6 / 3 = -2).
-
A negative number divided by a negative number results in a positive number (e.g., -6 / -3 = 2). The same sign rules as multiplication apply.
-
These sign rules in multiplication and division will be paramount in understanding how negative reciprocals function and why they behave the way they do.
Even with a strong grasp of basic reciprocals, understanding the nuances of negative reciprocals requires a solid foundation in negative numbers themselves. This understanding helps us visualize how these numbers behave and how they interact with the concept of inversion.
The Negative Reciprocal Rule: Finding Inverses with Ease
Finding the reciprocal of a negative number doesn’t need to be a source of frustration. The core principle is surprisingly straightforward: invert the number and maintain the negative sign. This section will provide a clear, step-by-step guide, complete with examples, to make mastering this concept a breeze.
The Cardinal Rule: Negative Reciprocal Sign Convention
The most fundamental rule to remember is this: the reciprocal of a negative number is always negative. This seemingly simple rule is the cornerstone of working with negative reciprocals. Grasping this concept prevents common errors.
Think of it this way: If a number is less than zero, its inverse will also be less than zero.
This consistency in sign makes calculations more reliable.
Step-by-Step Guide: Finding the Negative Reciprocal
Here’s a structured approach to finding the negative reciprocal of any number:
-
Start with the negative number. This is your initial value, the one you want to find the reciprocal of.
-
Express it as a fraction (if it’s not already). Whole numbers can be easily converted into fractions by placing them over 1 (e.g., -2 becomes -2/1).
-
Invert the fraction (swap the numerator and denominator). This means the top number becomes the bottom number, and vice versa.
-
Maintain the negative sign. This is the crucial step. Don’t forget to keep the negative sign in front of your inverted fraction.
Following these steps meticulously will lead you to the correct negative reciprocal every time.
Illustrative Examples: Practice Makes Perfect
Let’s solidify your understanding with a few practical examples:
Reciprocal of -2
-
Start with -2.
-
Express it as a fraction: -2/1.
-
Invert the fraction: -1/2.
-
The reciprocal of -2 is -1/2.
Reciprocal of -1/3
-
Start with -1/3.
-
It’s already a fraction.
-
Invert the fraction: -3/1 (which simplifies to -3).
-
The reciprocal of -1/3 is -3.
Reciprocal of -5/4
-
Start with -5/4.
-
It’s already a fraction.
-
Invert the fraction: -4/5.
-
The reciprocal of -5/4 is -4/5.
By working through these examples, you can see how straightforward the process becomes.
The key is consistent practice and attention to detail.
Even with a strong grasp of basic reciprocals, understanding the nuances of negative reciprocals requires a solid foundation in negative numbers themselves. This understanding helps us visualize how these numbers behave and how they interact with the concept of inversion.
Visualizing Reciprocals: The Number Line Connection
While abstract formulas and rules are essential, sometimes a visual aid can solidify understanding. The number line offers an intuitive way to grasp the relationship between a number and its reciprocal, especially when dealing with negative values.
Understanding Reciprocals on the Number Line
Imagine a number line stretching infinitely in both positive and negative directions. Zero sits at the center, acting as a crucial point of reference.
Positive reciprocals are relatively straightforward to visualize. For instance, 2 and 1/2 are reciprocals. On the number line, they both reside on the positive side, with 1/2 being closer to zero than 2.
The crucial point is that their relative positions help understand their inverse relationship. One is greater than 1, the other is less than 1.
Negative Reciprocals: Symmetry and Position
Negative reciprocals introduce an additional layer of understanding. Consider -2 and -1/2.
They are symmetrically positioned around zero compared to their positive counterparts.
-2 is the same distance from zero as 2, but on the negative side. Similarly, -1/2 mirrors 1/2 across zero.
This symmetry highlights the fact that the reciprocal operation maintains the sign; it only changes the magnitude.
The Special Case of -1
There’s one notable exception to the "different distance from zero" rule: the number -1. The reciprocal of -1 is also -1.
This is because -1 multiplied by itself equals 1, satisfying the definition of a reciprocal. On the number line, -1 is its own mirror image, residing at a unique fixed point.
Interpreting Distance and Magnitude
The distance of a number from zero on the number line represents its magnitude or absolute value. When visualizing reciprocals, notice how the reciprocal operation inverts this distance relative to 1.
A number greater than 1 will have a reciprocal between 0 and 1. Conversely, a number between 0 and 1 will have a reciprocal greater than 1.
With negative reciprocals, this principle applies in the negative domain. A number less than -1 will have a reciprocal between -1 and 0, and vice versa. This relationship is critical to internalize.
Visualizing reciprocals on the number line provides a powerful tool for building intuition and solidifying understanding. By observing the symmetrical placement of negative reciprocals and how their distances from zero relate, you can develop a deeper, more intuitive grasp of this fundamental mathematical concept.
Even with a strong grasp of visualizing reciprocals on a number line, the nuances of negative reciprocals requires careful attention to fractions. It’s one thing to conceptually understand the symmetry around zero, but another to confidently manipulate negative fractions and find their corresponding reciprocals. This section provides focused techniques to master the art of finding reciprocals of negative fractions.
Mastering Negative Fractions: Reciprocal Techniques
Working with negative fractions and their reciprocals can feel tricky, but by understanding the core principles, you can master this skill with confidence. The key is to remember the fundamental rule: when finding the reciprocal of any negative number, including fractions, you invert the number while always retaining the negative sign.
The Golden Rule: Invert and Retain the Negative Sign
The most important thing to remember is that the reciprocal of a negative number is always negative. This holds true whether you’re dealing with integers, decimals, or, most importantly, fractions. Forget this, and you’ll end up with the wrong answer.
Applying the Rule: Examples and Step-by-Step Breakdown
Let’s walk through some examples to solidify your understanding. We’ll break down each step to illustrate how the rule is consistently applied.
Example 1: Finding the Reciprocal of -2/3
- Start with the negative fraction: -2/3
- Invert the fraction: This means swapping the numerator (2) and the denominator (3). The inverted fraction is 3/2.
- Retain the negative sign: Since we started with a negative fraction, the reciprocal is also negative. Therefore, the reciprocal of -2/3 is -3/2.
Example 2: Finding the Reciprocal of -7/5
- Start with the negative fraction: -7/5
- Invert the fraction: Swap the numerator (7) and the denominator (5) to get 5/7.
- Retain the negative sign: The reciprocal of -7/5 is -5/7.
Example 3: Finding the Reciprocal of -1/8
- Start with the negative fraction: -1/8
- Invert the fraction: Inverting 1/8 gives us 8/1, which is simply 8.
- Retain the negative sign: The reciprocal of -1/8 is -8. Notice that -8 can also be written as the fraction -8/1.
Sign Consistency: A Non-Negotiable Rule
It’s worth reiterating: when inverting a negative fraction, never change the sign.
The negative sign is an integral part of the number and must be carried through the reciprocal operation. Changing the sign would result in finding the additive inverse (the opposite) rather than the multiplicative inverse (the reciprocal). Keep the sign consistent, and you’ll consistently find the correct reciprocal.
Why This Matters: Real-World Applications of Negative Reciprocals
Even with a strong grasp of visualizing reciprocals on a number line, the nuances of negative reciprocals requires careful attention to fractions. It’s one thing to conceptually understand the symmetry around zero, but another to confidently manipulate negative fractions and find their corresponding reciprocals. This section provides focused techniques to master the art of finding reciprocals of negative fractions.
But why dedicate so much effort to mastering negative reciprocals? This knowledge isn’t just an abstract mathematical exercise; it’s a fundamental tool with widespread applications across various fields. Understanding negative reciprocals opens doors to solving complex problems and gaining a deeper appreciation for the interconnectedness of mathematics and the world around us.
The Value of Understanding Negative Reciprocals
The understanding of negative reciprocals extends far beyond the classroom. It’s crucial for problem-solving in advanced mathematics, various scientific disciplines, and even everyday financial calculations. Grasping this concept sharpens your analytical abilities, allowing you to approach problems with increased confidence and precision.
Negative Reciprocals in Advanced Mathematics
Algebra
In algebra, negative reciprocals are instrumental in solving equations involving slopes of perpendicular lines. Two lines are perpendicular if and only if the product of their slopes is -1. This geometric relationship is directly defined by negative reciprocals.
For instance, if a line has a slope of 2/3, a line perpendicular to it will have a slope of -3/2. Understanding this connection is essential for solving geometric problems and understanding coordinate geometry.
Calculus
Calculus leverages negative reciprocals in understanding derivatives and rates of change. For example, when dealing with inverse functions, the derivative of the inverse function at a point is the reciprocal of the derivative of the original function at the corresponding point. This relationship can often involve negative values, making the understanding of negative reciprocals absolutely crucial.
Physics and Engineering
Negative reciprocals frequently appear in physics and engineering calculations, especially in areas dealing with oscillations and waves. Understanding impedance, reactance, and admittance in electrical circuits, for example, relies on the ability to manipulate complex numbers and their reciprocals, which often involve negative components. This is critical for designing stable and efficient electronic systems.
Division Using Reciprocals: Multiplication by the Inverse
One of the most powerful applications of reciprocals, including negative reciprocals, lies in simplifying division. Dividing by a number is mathematically equivalent to multiplying by its reciprocal.
This principle is not merely a mathematical trick; it simplifies complex calculations and offers a different perspective on division.
Consider the problem of dividing 10 by -2/3. Instead of directly performing the division, you can multiply 10 by the reciprocal of -2/3, which is -3/2.
The calculation becomes:
10 * (-3/2) = -15.
This transformation of division into multiplication can streamline complex calculations, especially when dealing with fractions or algebraic expressions. It’s a foundational tool in simplifying equations and solving problems efficiently.
In conclusion, the mastery of negative reciprocals is not merely an academic exercise. It’s a gateway to deeper understanding and problem-solving capabilities across a multitude of disciplines. From algebra and calculus to physics and everyday calculations, the ability to confidently manipulate negative reciprocals is an invaluable skill.
The ability to manipulate negative reciprocals smoothly unlocks doors to advanced mathematical problem-solving. Before you confidently solve for perpendicular slopes or tackle complex equations, it’s prudent to highlight the common slip-ups that can easily derail your progress. Recognizing these pitfalls is half the battle, empowering you to sidestep these traps and reinforce your understanding.
Avoiding Common Pitfalls: Stay Sharp
Mastering negative reciprocals involves not only understanding the rules but also avoiding the common mistakes that can trip up even seasoned math students. This section is dedicated to highlighting these pitfalls, offering strategies to recognize and avoid them, ensuring you stay sharp and accurate in your calculations.
The Case of the Missing Negative Sign
One of the most frequent errors is forgetting to retain the negative sign when finding the reciprocal. Remember, the reciprocal of a negative number is always negative, and vice-versa.
Forgetting this simple fact leads to incorrect answers and misunderstandings of the underlying mathematical principles.
A good strategy is to write down the negative sign immediately after writing down the original number. This serves as a visual reminder throughout the inversion process.
For example, if you’re finding the reciprocal of -3/4, immediately write down "-", then proceed to invert the fraction to 4/3, resulting in -4/3. This visual cue is a powerful habit to develop.
Fraction Flubs: Inversion Errors
Another common mistake lies in incorrectly inverting the fraction. This typically happens when students rush through the process or become confused by complex fractions.
Double-check your work to ensure that the numerator and denominator have been properly swapped.
A simple method is to rewrite the fraction step-by-step.
For instance, to find the reciprocal of -5/2, rewrite it as -(2/5) to avoid any confusion. Visualizing the swap can prevent errors.
Reciprocal vs. Additive Inverse: Know the Difference
Perhaps the most conceptually challenging error is confusing a reciprocal with an additive inverse, also known as the opposite.
The reciprocal of a number, when multiplied by the original number, results in 1. The additive inverse, when added to the original number, results in 0. These are fundamentally different concepts.
For example, the reciprocal of -2 is -1/2, because (-2) * (-1/2) = 1. The additive inverse (opposite) of -2 is 2, because (-2) + 2 = 0.
Always remember to ask yourself: "Does multiplying these two numbers yield 1?" if you’re finding a reciprocal, and "Does adding these two numbers yield 0?" if you’re finding an additive inverse.
Understanding the distinction is crucial for avoiding confusion and applying the correct mathematical principles in various contexts.
Negative Number Reciprocals: Frequently Asked Questions
Here are some common questions about reciprocals of negative numbers to help you better understand the concept.
What exactly is the reciprocal of a negative number?
Finding the reciprocal of a negative number is the same as finding the reciprocal of a positive number, but keeping the negative sign. For example, the reciprocal of -2 is -1/2. It’s just flipping the fraction and maintaining the negativity.
How do I find the reciprocal of a negative fraction?
To find the reciprocal of a negative fraction, flip the numerator and denominator and keep the negative sign. For instance, the reciprocal of -3/4 is -4/3. Remember the reciprocal of a negative number will always be negative.
Is the reciprocal of a negative number always a fraction?
No, the reciprocal of a negative number isn’t always a fraction. If you start with a negative fraction, its reciprocal will also be a fraction. However, if you start with a negative whole number (like -5), its reciprocal will be a fraction (-1/5).
Does a negative number have the same reciprocal as its positive counterpart, but with a negative sign?
Yes, precisely. The reciprocal of negative number is the negative version of the reciprocal of its positive counterpart. For instance, the reciprocal of 3 is 1/3, and the reciprocal of -3 is -1/3.
And there you have it! Hopefully, you now feel confident tackling the reciprocal of negative number. Go forth and multiply… or should we say, take the reciprocal?